de periode-helderheidsrelatie van pulserende RR Lyrea sterren
Ik heb geprobeerd aan de hand van helderheidsmetingen van pulserende sterren in Messier 3 de afstand tot deze bolhoop te bepalen. Deze bolhoop bevind zicht in het sterrenbeeld Cannes Venetici (CVn)
Lang verhaal kort: het is niet gelukt. De periode-helderheidsrelatie voor deze sterren in de groene (V) band is niet zo goed. Maar ik weet wel wat ik nodig heb om een betere poging te wagen. Een nieuw infrarood filter.

In maart en april 2022 heb ik 4 nachten de bolhoop Messier 3 opgenomen. De bedoeling de eerste nacht was te kijken hoeveel variabele sterren ik hierin kan oppikken, gebruik makend van fotometrie. Nou dat is goed gelukt! Maar liefst 16 sterren in mijn fotometrische analyses vertonen hele duidelijke variabiliteit.
Dit bleken op één na allemaal pulserende sterren te zijn met een periode van rond 12 uur. Omdat ik in deze tijd van het jaar niet een hele cyclus kan vangen in 1 nacht had ik besloten om meerdere nachten te gaan waarnemen. En dan alleen in Luminance (UV/IR cut filter). Dit omdat het signaal in de R, G en B filters te laag was om goede metingen van te maken.
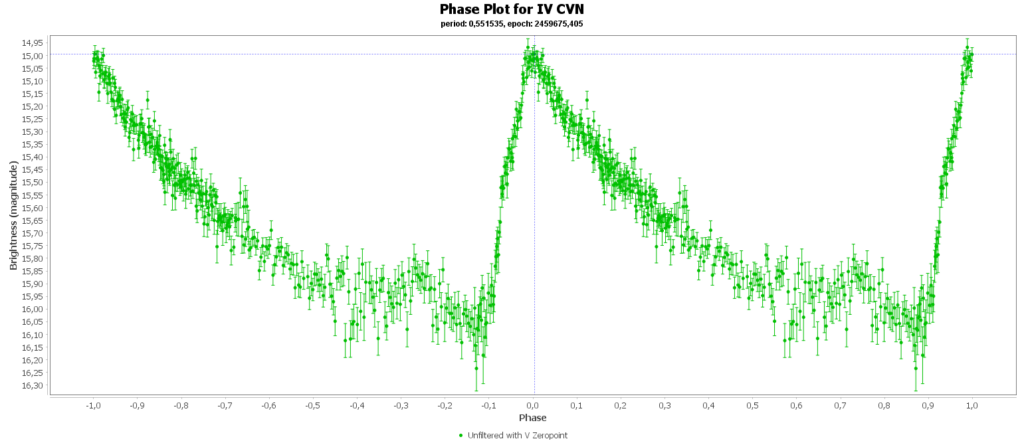
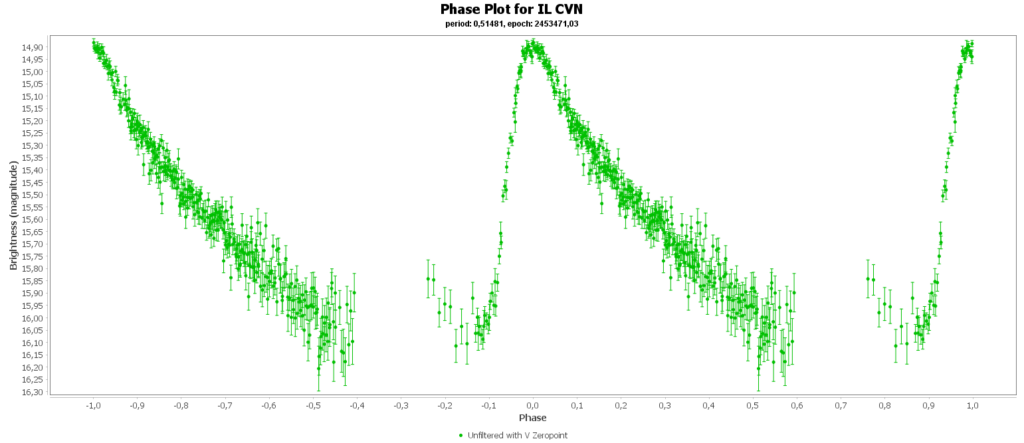
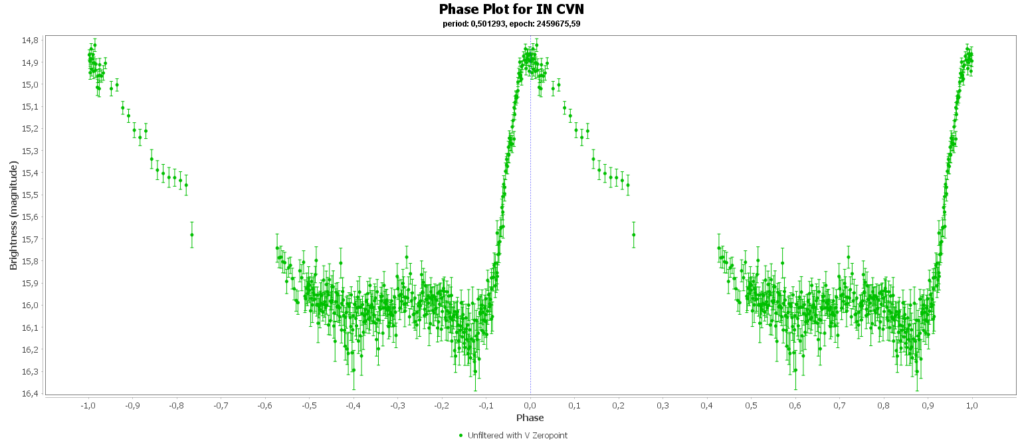
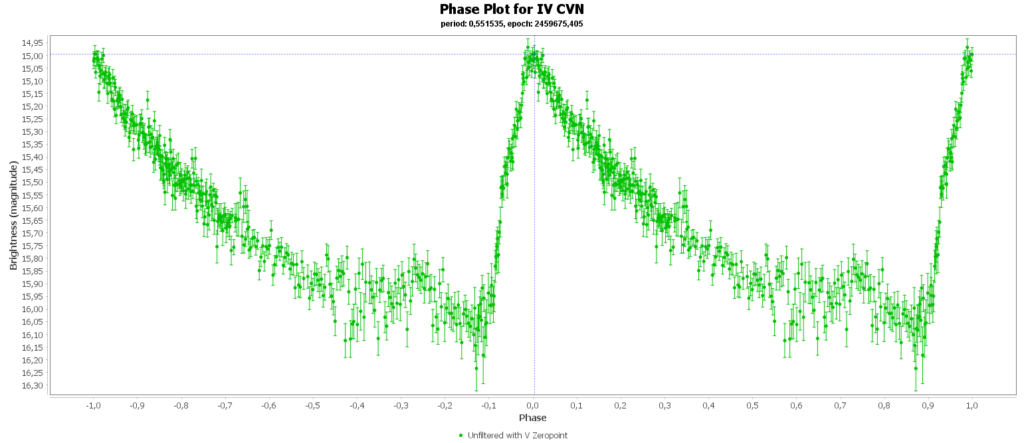
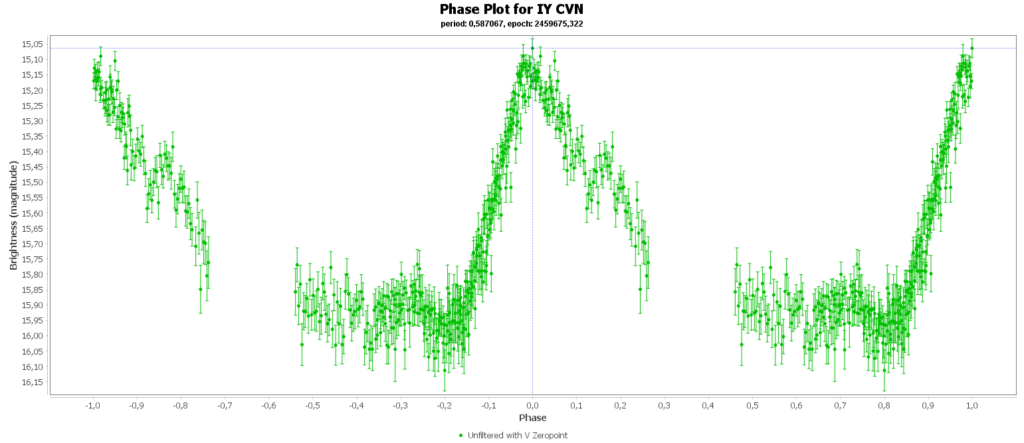
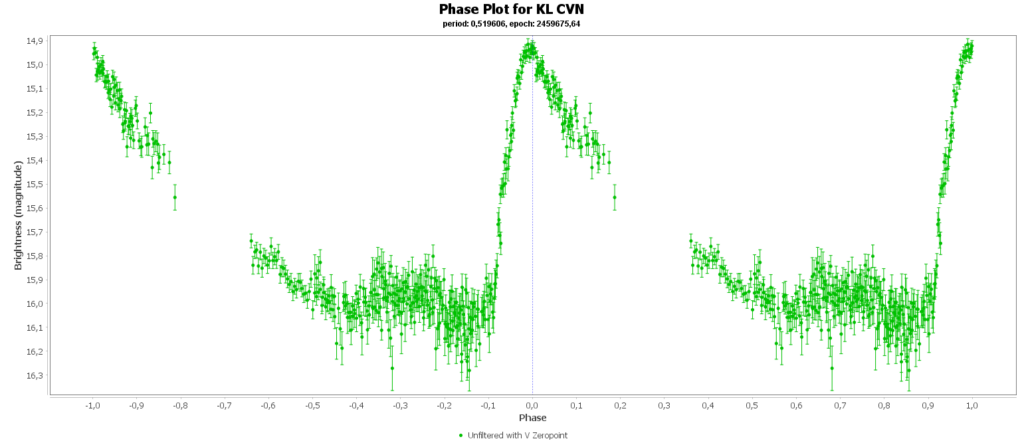
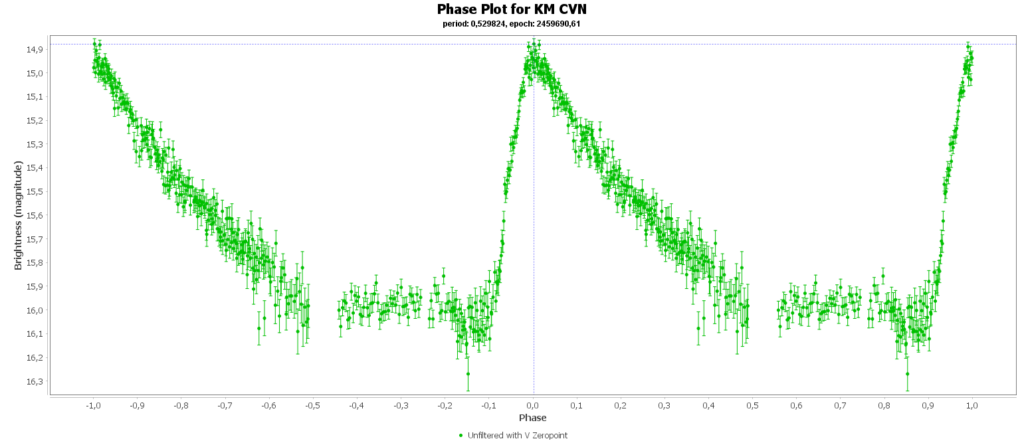
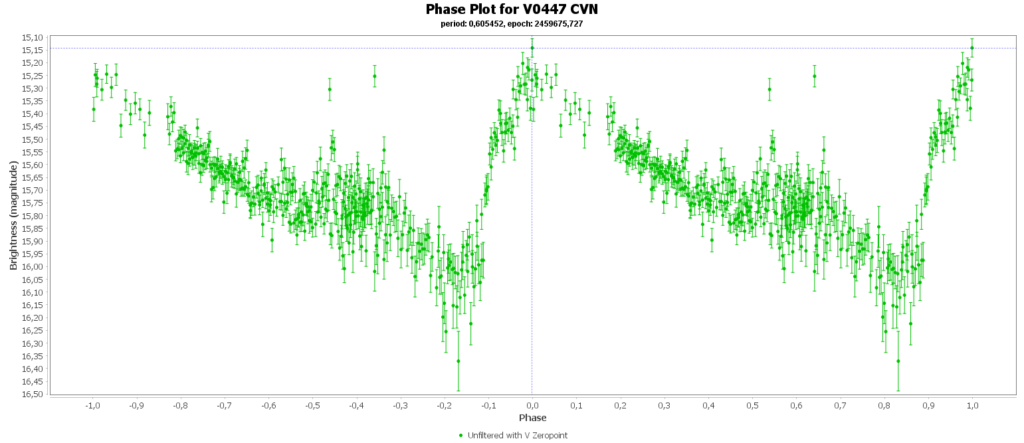
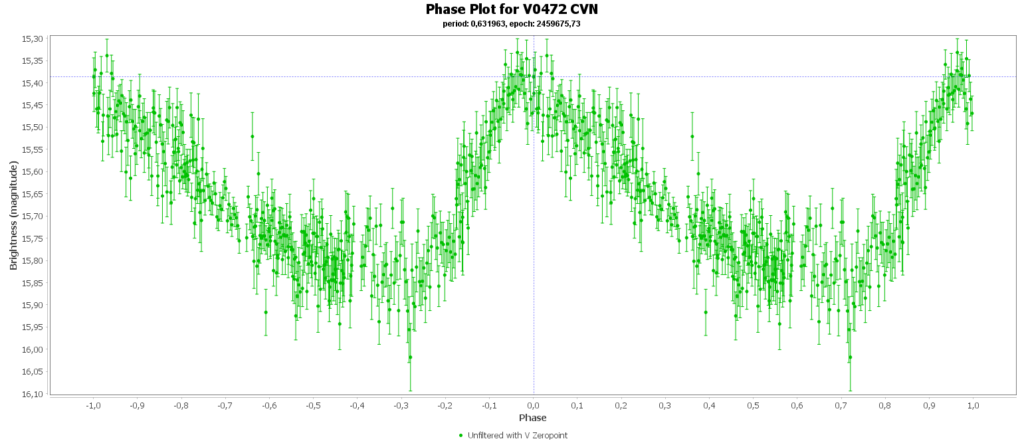
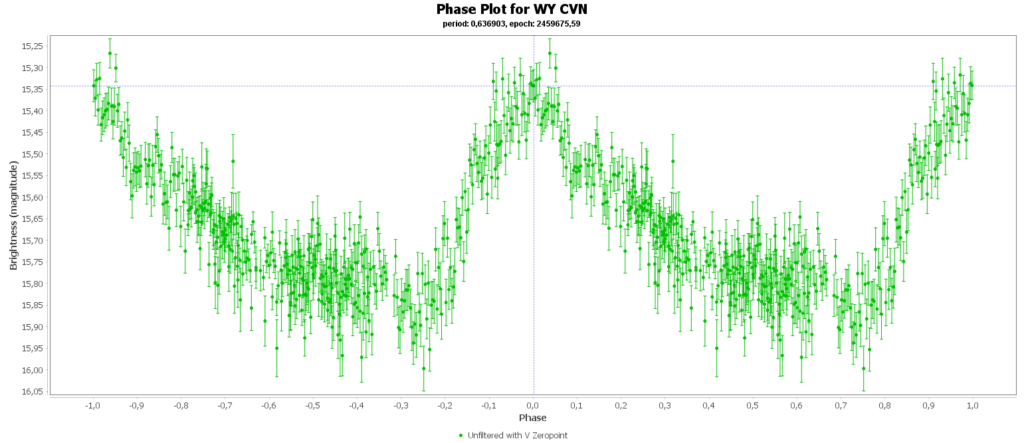
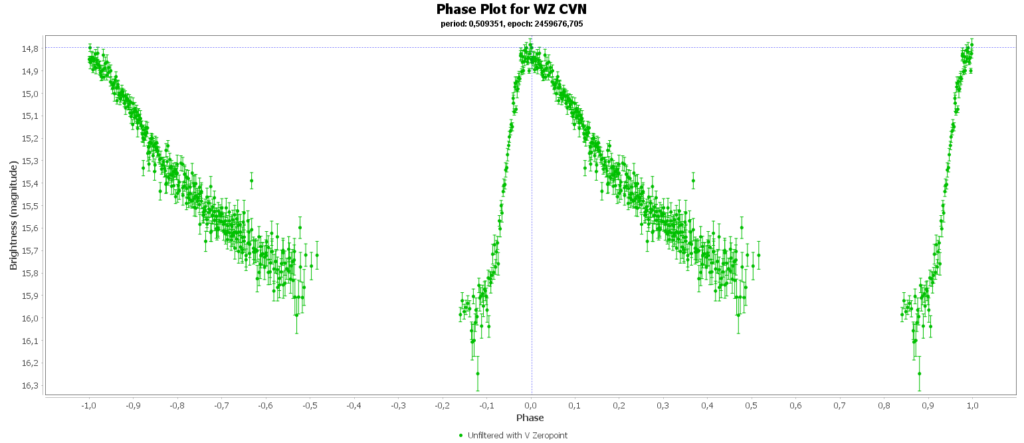
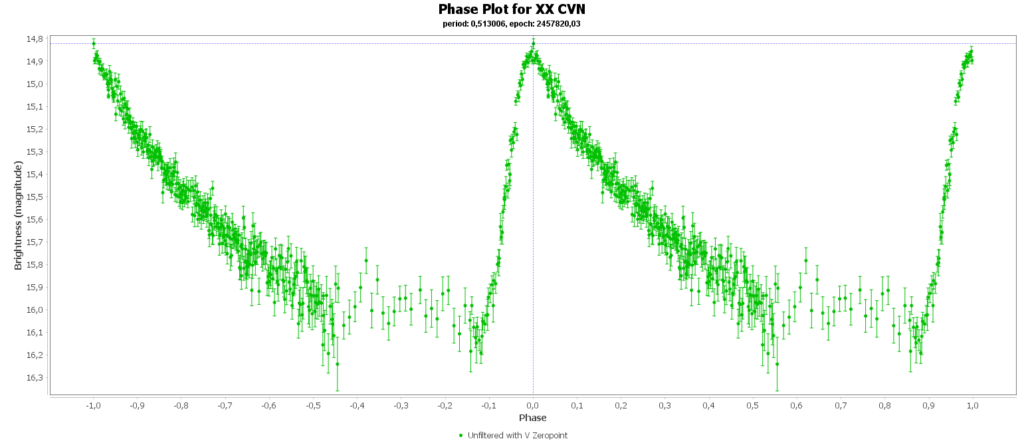
Om de metingen van meerdere nachten te combineren tot 1 mooie lichtcurve per ster, heb ik het softwarepakket Vstar van de AAVSO (American Association of Variable Star Observers) gebruikt. Daarmee kun je uit je data de periode analyseren, en daarna de metingen met die periode over elkaar heen vouwen, tot een faseplot. Zo kun je losse stukjes van een lichtcurve tot een volledige lichtcurve combineren. Dat ziet er zo uit:
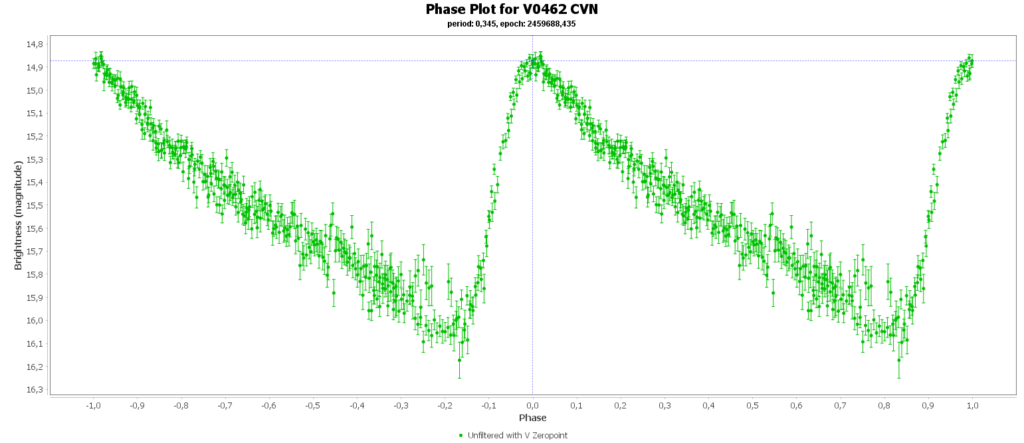
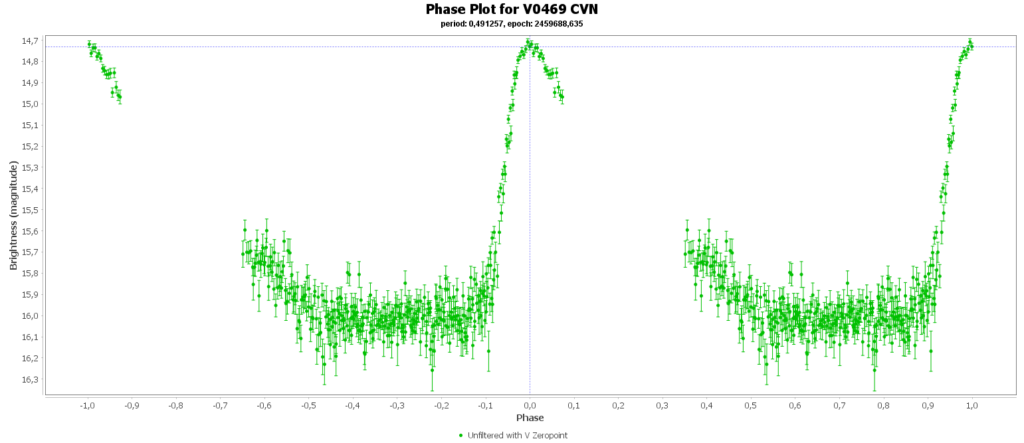
Bij sommigen zie je dan nog steeds gaten zitten in de faseplot. Die sterren hadden en periode heel dicht rond de 12 uur. Als je dan meerdere nachten waarneemt, dan zit je elke keer in het zelfde stuk van de cyclus en mis je dus helaas ook stukken.
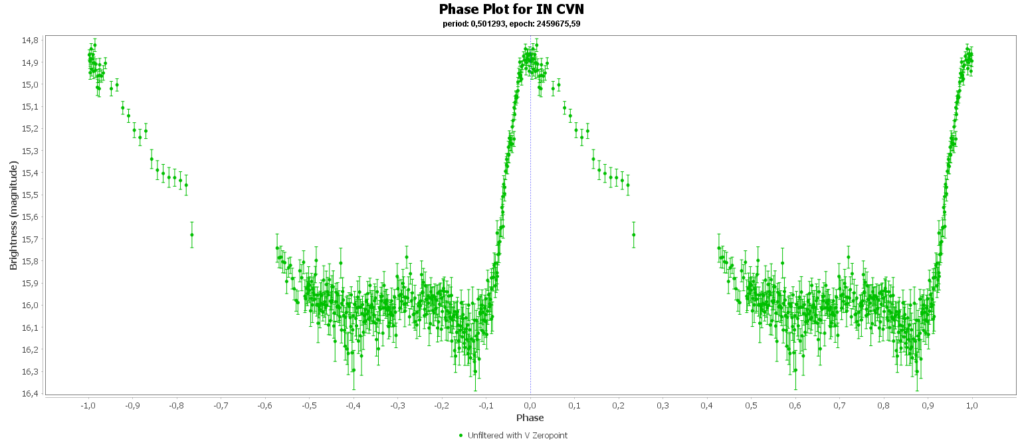
Aan het einde van deze pagina zijn alle door mij gegenereerde fase plots in een galerij verzameld.
Animatie
Als bonus kon ik van de opname van in nacht ook een animatie maken. Daarbij heb ik elke keer 10 opname van 3 minuten tot 1 frame gecombineerd. Dat resulteerde in een loop die 6,5 uur representeert. dus 13 frames van 30 minuten. In de animatie zie je veel meer dan 15 sterren pulseren. Dit komt doordat ik alleen in de buitenranden van het cluster goede fotometrische analyses kon doen. In het midden zitten de sterren daarvoor te dicht opeen gepakt.


RR Lyrea pulserende sterren
Al deze pulserende in Messier 3 blijken RR Lyrea sterren te zijn. RR Lyrea sterren zijn pulserende sterren met een periode tussen grofweg 6 uur tot 2 dagen. Binnen de RR Lyrea sterren zijn drie subklassen te vinden.
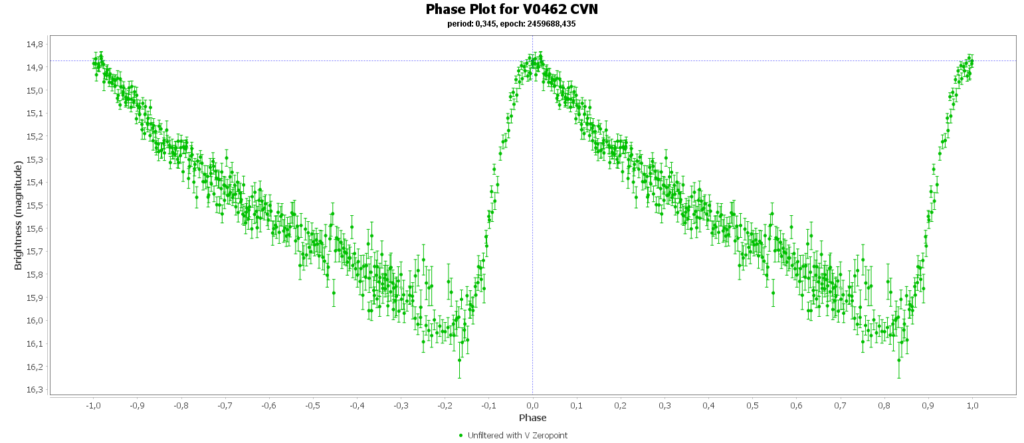
Deze meest voorkomende is de RRab subklasse (90% van het totaal). De meeste in mijn metingen zijn ook van dit type. In mijn geval 13 van de 15. Deze hebben een mooie scherpe piek, en als bonus is dit type ook het best te gebruiken als afstand indicator doordat deze de beste periode-afstandsrelatie vertonen. Maar daarover hierna meer.
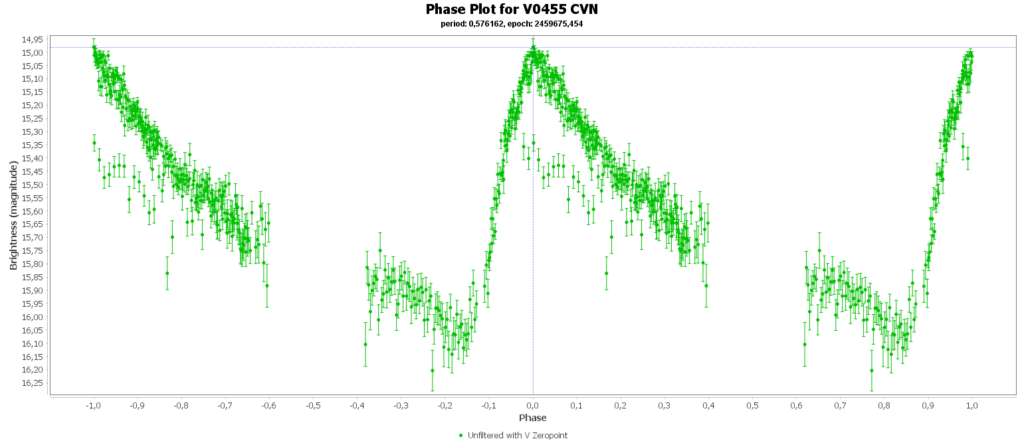
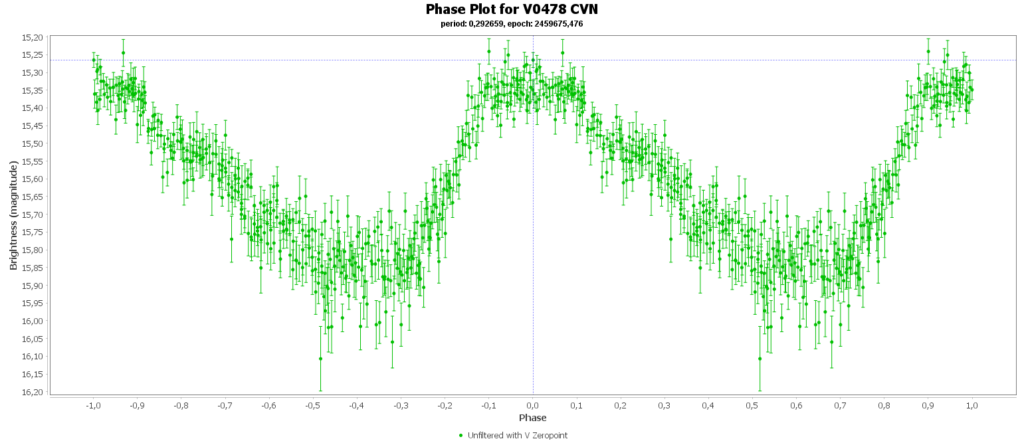
Dan zijn er nog de RRc sterren met ongeveer 9% van het totaal. In mijn geval 2 van de 15. Die hebben vaak een iets kortere periode en de vorm van de curve is ook iets anders, meer een sinus achtige curve. Ze hebben vaak ook periode en amplitude modulaties doordat ze in meerdere modussen pulseren, met boventonen als gevolg. zoals deze:
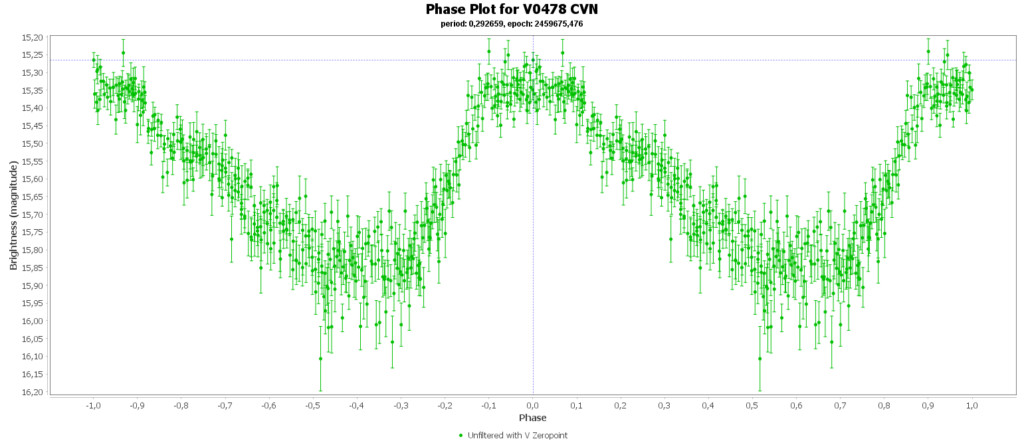
Dan is er nog de RRd subklasse
Periode-helderheid relatie van sterren op de instabiliteitsstrip.
RR Lyrea sterren hebben dus net als andere pulserende sterren, zoals Cepheïden, een periode-helderheidsrelatie. Dit betekent dat als je de periode weet, en de schijnbare helderheid, dat je de afstand tot de ster kunt terugrekenen. Edwin Hubble heeft bijvoorbeeld in 1928 met behulp van een Cepheïden de afstand tot de andromeda nevel bepaalt en daarmee bewezen dat deze ver buiten de Melkweg ligt. Daarmee was bewezen dat er meerdere melkwegstelsels bestaan.
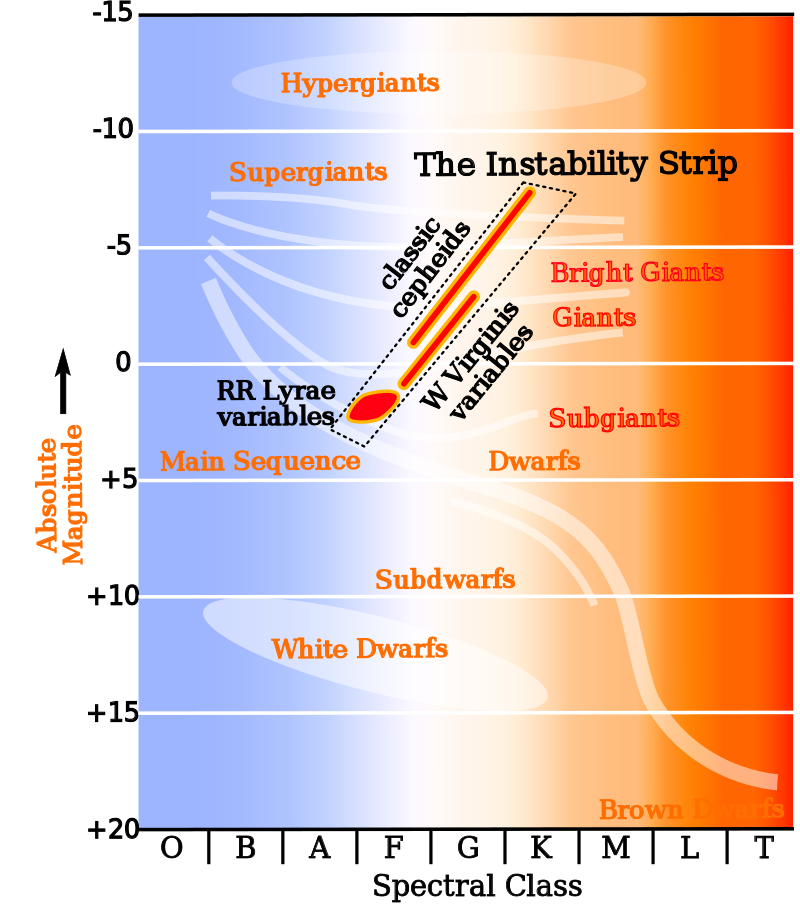
In het Hertzsprung-Russel diagram zijn meerdere type sterren te vinden die een dergelijke periode-helderheidsrelatie hebben. Deze bevinden zich op de instabiliteitsstrip.
Deze sterren pulseren doordat precies op de goede diepte in de ster helium geïoniseerd wordt bij waardoor die laag minder transparant wordt (Kappa mechanisme). Daardoor duwt de lichtkracht onder die laag de ster uiteen.
De pieken die je ziet in de lichtcurves zijn de momenten waar de ster het kleinst in diameter is. Door de compressie van het gas is de temperatuur hoger en is de ster feller.

In het kappa-mechanisme wisselt helium tussen enkelvoudig en 2-voudig geïoniseerd bij een specifieke temperatuur. He2+ wordt gevormd als helium verhit wordt door de compressie van de laag. Dat maakt die laag van de ster minder transparant en zorg ervoor dat de ster uitzet. Als de ster uitzet, koelt deze laag weer af en wordt He2+ weer He+. De schil wordt weer transparant, het licht ontsnapt en de ster krimpt weer ineen. En zo herhaalt de cyclus zich
Poging de afstand tot Messier 3 te bepalen
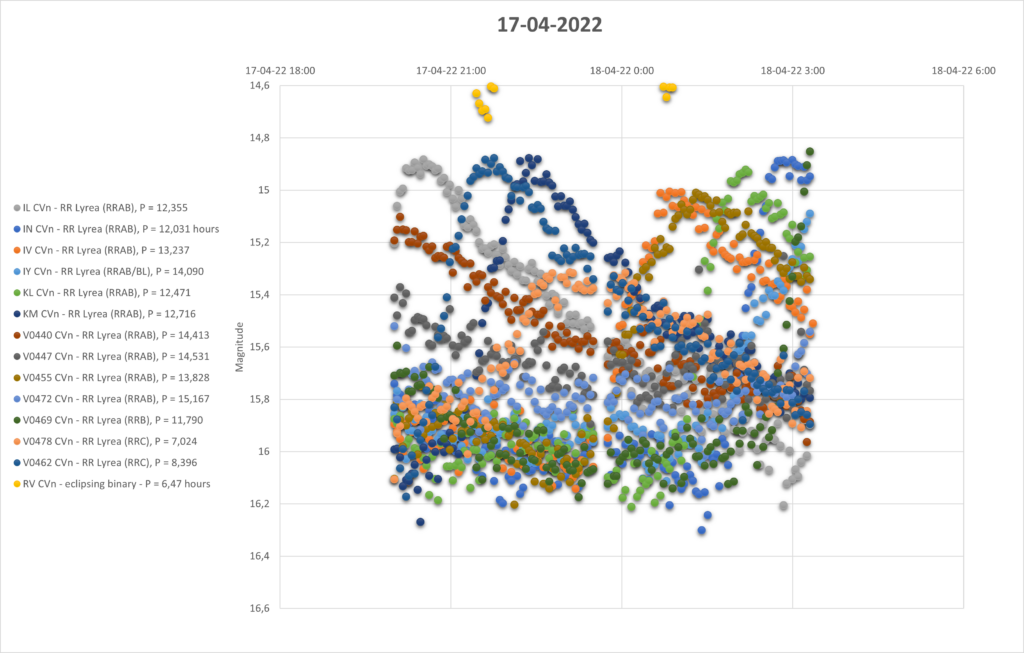
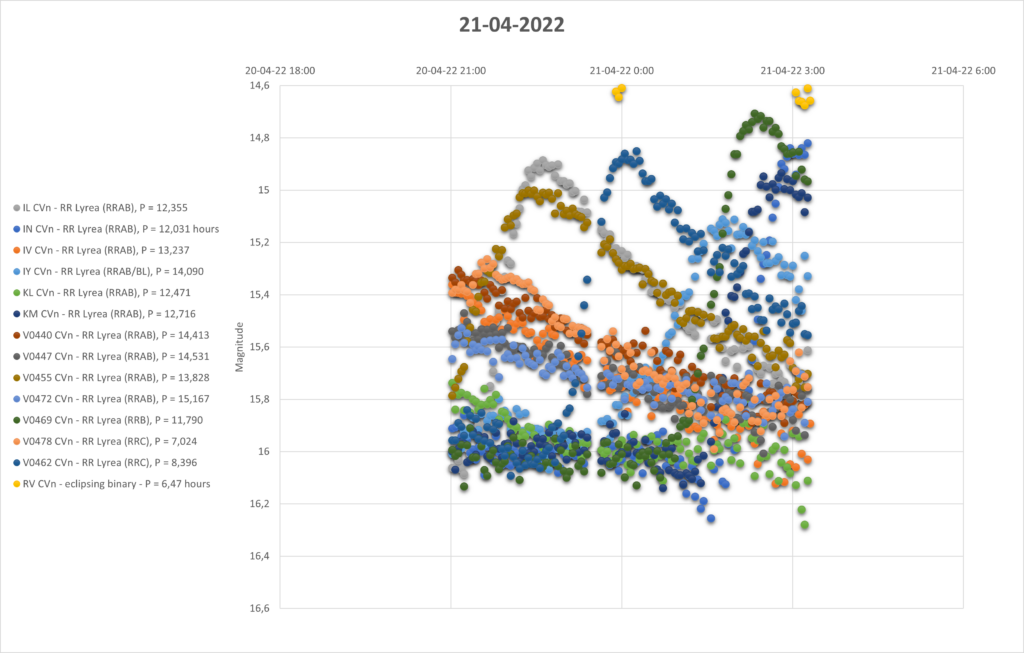
Dus ik dacht; Mooi! Dat ga ik ook doen met dit cluster. Ik heb daarvoor nog eens 3 nachten met een L filter het cluster opgenomen. Hieronder zie je de lichtcurves van de losse waarneemdagen, van alle 15 sterren door elkaar heen.
Je ziet dat ze allemaal ongeveer de zelfde helderheid hebben, en alle sterren in de RRab klasse hebben een periode van ongeveer 12 uur, dus dat lijkt veel belovend.

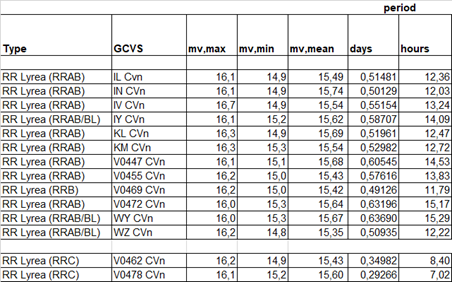
Om met de periode-helderheidsrelatie de afstand tot het cluster te bepalen heb je de gemiddelde helderheid per ster nodig. Dus die heb ik berekend per ster. Dit kan niet zomaar door alle metingen uitgedrukt in magnitude te middelen. De magnitude is namelijk logaritmisch, elke magnitude is een verschil in helderheid met een factor 2,51. Eerst moet je elke meting dus omrekenen naar een flux om alle metingen lineair met elkaar vergelijkbaar te maken. Van de flux per meting kun je het gemiddelde nemen en dan weer terugrekenen naar een gemiddelde magnitude. Dit heb ik gedaan voor de RR Lyrea sterren in mijn opnamen.
Toen ik dat had dacht ik, laat ik de periode maar eens tegen de schijnbare helderheid plotten. Die zou immers een duidelijke relatie moeten laten zien. En dan wel één waarbij een kortere periode een lagere helderheid moet geven, en dus een hogere magnitude).
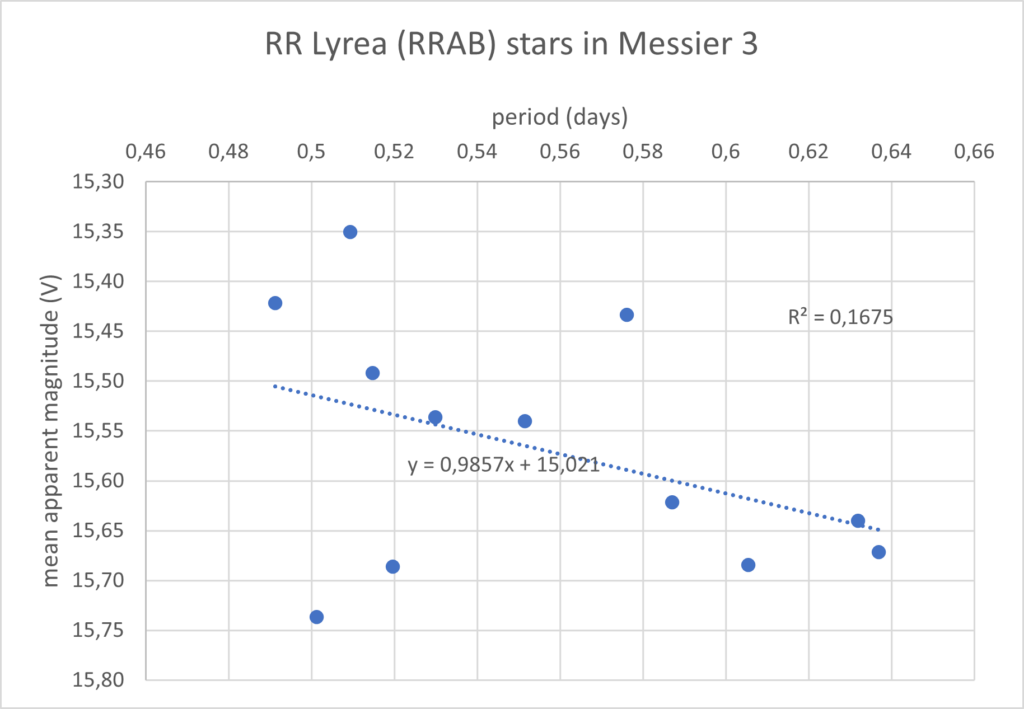
Wat schetst mijn verbazing, de relatie loopt de andere kant op! Als er überhaupt al een relatie te zien is. De determinatie coëfficiënt ‘R2’ is namelijk heel laag (0,1675). Dit is een maat voor hoe goed de relatie van de metingen tot de trendlijn van die metingen is. 1 is een perfecte relatie en 0 is geen enkele relatie. 0,1675 is dus niet echt best.
Daarna ben ik terug gegaan naar google en heb ik een aantal onderzoeksartikelen opgezocht hierover. Meerdere artikelen geven aan dat de periode-helderheidsrelatie van RR Lyrea in de groene band (V-band) heel onstabiel is. Mijn metingen zijn in de V-band genomen.
Ik kan ook geen artikel vinden die zich eraan waagt een periode-helderheidsrelatie in de groene band te benoemen.
Bij wijze van experiment heb ik nog wel de periode-helderheidsrelatie van de klassieke Cepheïden in de V-band gebruikt. Dit is de wet van Leavitt, vernoemd naar Henrietta Leavitt die deze relatie in 1908 heeft opgesteld. Met de onderstaande vergelijking bereken je de absolute magnitude aan de hand van de periode van de ster.
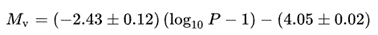
Vervolgens bereken je de afstand tot de ster door de volgende vergelijking. Daarmee bereken je uit het verschil tussen de absolute magnitude (M) en de gemeten schijnbare magnitude (m) de afstand tot de ster:
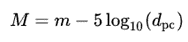
mv is de gemeten schijnbare helderheid
dpc is de afstand tot de ster in parsec. Één parsec is 3,262 lichtjaar.
Als ik dit doe voor de 12 RRab sterren, dan kom ik op ongeveer 66.000 lichtjaar. Dat is er een factor 2 naast, want Messier ligt op circa 34.000 lichtjaar.
Betere relatie in infrarood banden
Wat ik wel kan vinden in de onderzoeksartikelen is de verklaring voor deze afwijking. De periode-helderheidsrelatie is er wel voor RR Lyrea sterren, maar in het infrarood!
Hoe verder in het infrarood hoe beter de relatie wordt blijkt. De groene V-band wordt wel gebruikt in het onderzoek, maar enkel om de metaliciteit van de sterren te bepalen. Deze heeft ook weer invloed op de pulsatieperiode. Kort verhaal lang, het is allemaal niet zo eenvoudig als ik dacht.
Deze figuur hieronder uit 1 van de artikelen geeft heel mooi weer waardoor ik geen duidelijke relatie kan vinden in de V-band.
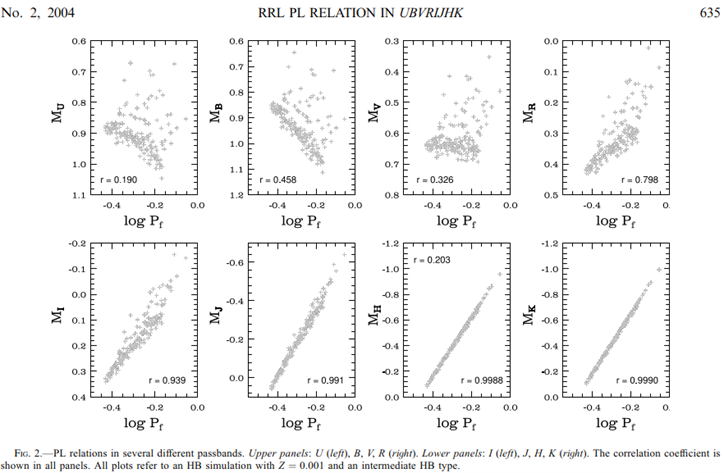
In de UV, blauwe en groene band (U,B en V) is de relatie op zijn zachtst gezegd wiebelig, en bij UV en blauw ook omgekeerd. Vanaf rood (R) wordt het beter, en vanaf infrarood (I) is hij behoorlijk mooi, met een R2 rond 0,88 (r van 0,939 in het kwadraat), dus een redelijk sterke relatie.
Deze periode-helderheidsrelaties uitgedrukt zoals hieronder. De relatie in het infrarood kan ik wel gebruiken. Mijn camera is prima instaat om de I-band op te pikken, en er zijn fotometrische I-filters verkrijgbaar voor amateurs. Deze worden ook veelvuldig gebruikt door amateurs. De overige banden (J, H en K) zitten verder in het infrarood en worden niet opgepikt door de gangbare CMOS en CCD camera’s die de gemiddelde amateur gebruikt.

In de relaties zie je ook ‘Z’ staan. Dit is de metaliciteit van een betreffende ster. Dit is simpel gezegd de fractie van het materiaal in de ster dat geen waterstof of helium is. In de astronomie wordt namelijk alles behalve waterstof en helium een metaal genoemd.
Voor hele oude sterren in bolhopen is dit typisch maximaal 0,002. De zon is van een latere generatie en heeft een Z van circa 0,02 dus die is al veel rijker aan ‘metalen’. Daardoor hebben er bij ons ook steenachtige planeten kunnen vormen en zijn die er in bolhopen zeer waarschijnlijk niet.
Conclusie
Wat staat mij nu dus te doen? Een fotometrische infrarood (I) filter aanschaffen en de hele oefening nog eens herhalen! Ik was toch al van plan om dat ooit te doen. Dus dit lijkt me een goed excuus.
Wordt vervolgd wanneer het I filter binnen is 🙂
Dubbele bonus
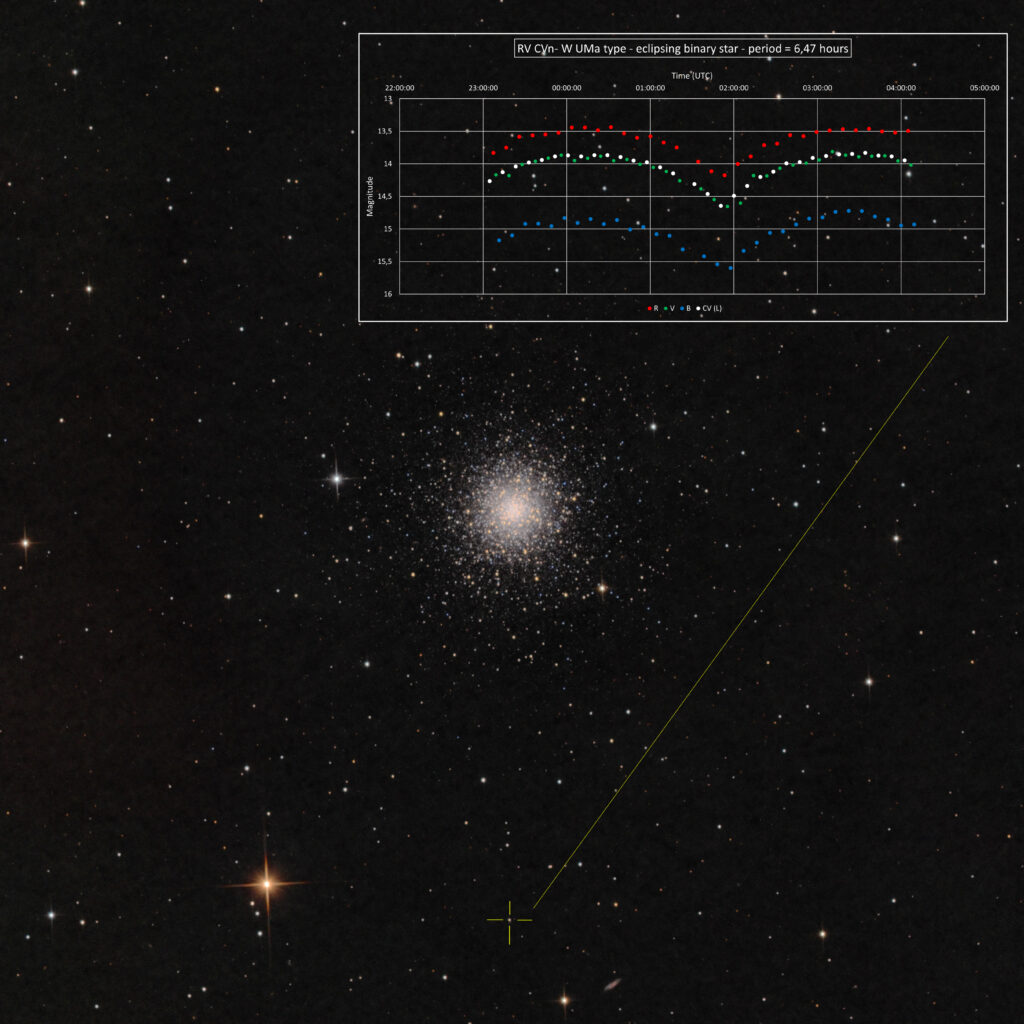
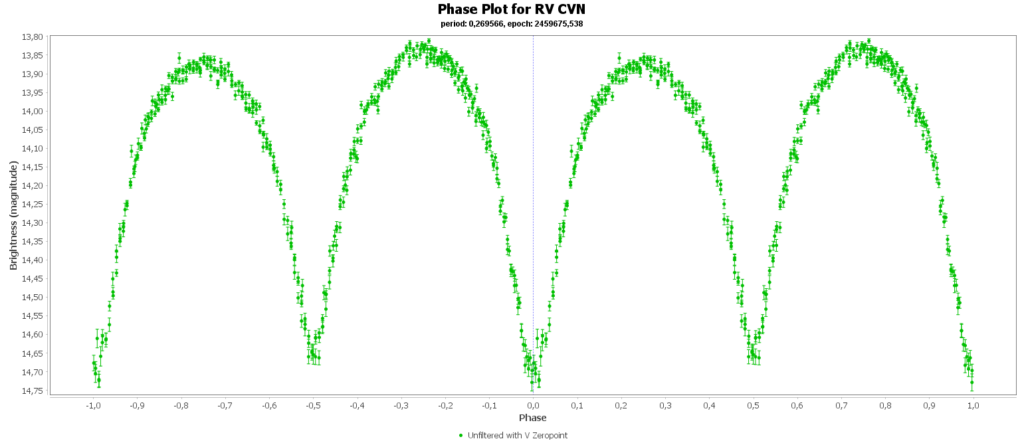
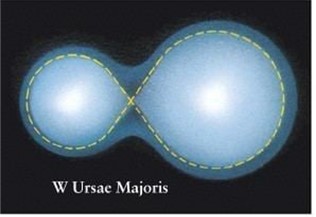
In het beeldveld zat nog een bonus, van de bedekkingsvariabele dubbelster RV CVn. Dit zijn 2 voorgrondsterren die zich niet in de bolhoop bevinden. Ze draaien in een periode van 6,47 uur om elkaar. In die tijd vertoond het systeem 2 dips doordat de sterren voor elkaar langs bewegen vanuit ons oogpunt. Daarbij wordt een deel van het licht geblokkeerd. De sterren zijn sterk vervormd doordat ze zo dicht bij elkaar staan. Hierdoor verandert de helderheid voortdurend, doordat de hoeveelheid oppervlak van het systeem dat wij zien telkens verandert.